In this article we will learn about Prime Number in csharp. Prime numbers are natural numbers that are divisible by only 1 and the number itself. In other words, prime numbers are positive integers greater than 1 with exactly two factors, 1 and the number itself. Some of the prime numbers include 2, 3, 5, 7, 11, 13, etc.
Always remember that 1 is neither prime nor composite. Thus, all prime numbers are greater than 1. Also, we can say that except for 1, the remaining numbers are classified as prime and composite numbers. In this article, we will learn how to get prime number programming in c#. Please read our previous article Palindrome in C#.
Prime Number in csharp
Today in this article I will share you how to create Prime number in C#. This is the common question of any interviewer if you are fresher. So I explain in details what is prime number and how to check the number is prime or not.
What is Prime Number?
A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself.
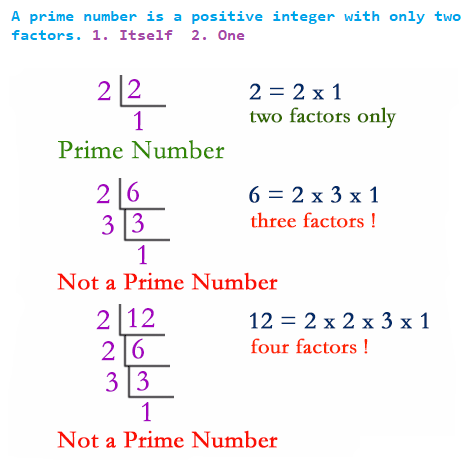
Example:
using System;
namespace PrimeNumber
{
class Program
{
static void Main(string[] args)
{
Console.WriteLine("Enter a number");
int number = Convert.ToInt32(Console.ReadLine());
int result = Check_Prime(number);
if (result == 0)
{
Console.WriteLine("{0} is not a prime number", number);
}
else
{
Console.WriteLine("{0} is a prime number", number);
}
Console.Read();
}
private static int Check_Prime(int number)
{
int i;
for (i = 2; i <= number - 1; i++)
{
if (number % i == 0)
{
return 0;
}
}
if (i == number)
{
return 1;
}
return 0;
}
}
}Output:
Enter the Number to check Prime: 13 Number is Prime.
Enter the Number to check Prime: 41 Number is not Prime.
Points to Remember
The only even prime number is 2. All other even numbers can be divided by 2.
If the sum of a number’s digits is a multiple of 3, that number can be divided by 3.
No prime number greater than 5 ends in a 5. Any number greater than 5 that ends in a 5 can be divided by 5.
Zero and 1 are not considered prime numbers.
Except for 0 and 1, a number is either a prime number or a composite number. A composite number is defined as any number, greater than 1, that is not prime.
To prove whether a number is a prime number, first try dividing it by 2, and see if you get a whole number. If you do, it can’t be a prime number. If you don’t get a whole number, next try dividing it by prime numbers: 3, 5, 7, 11 (9 is divisible by 3) and so on, always dividing by a prime number (see table below).Here is a table of all prime numbers up to 1,000:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 |
| 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 |
| 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 |
| 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 |
| 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 |
| 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 |
| 349 | 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 |
| 409 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 |
| 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 |
| 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 |
| 659 | 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 |
| 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 |
| 809 | 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 |
| 863 | 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 |
| 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Hope It will clear about the Prime Number. Still have any question regarding this, Please have give feedback.
